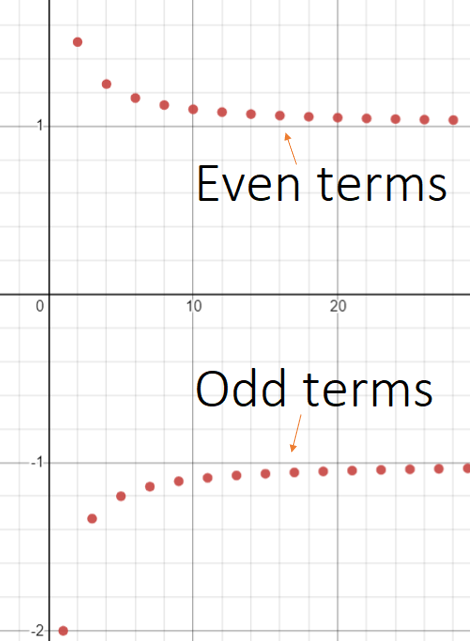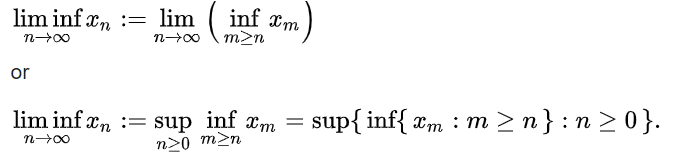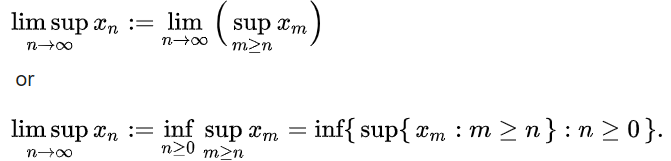Contents:
Subsequential Limits
A subsequential limit is the limit of a subsequence; a subsequence is a smaller part of some larger sequence. For example, the integer sequence {1, 2, 1, 2} has two subsequences: one for odd numbers and one for even numbers.
Sometimes a limit doesn’t exist for a sequence, but does exist for one or more subsequences. For example, the limit for the following sequence doesn’t exist:
However, there are three subsequences with limits [1]:
- (x1, x4, x7, …) converges to 1.
- (x2, 51, 81, …) converges to 0.
- (x3, x6, x9, …) converges to -1.
Examples: Finding a Subsequential Limit
Example question #1: Find the subsequential limits of the sequence an = 1 – (-1)n.
The key here is to look for a pattern by generating some terms.
Step 1: Generate some terms of the sequence. One of the easiest ways to do this is in Excel. Here’s the steps:
- Type the numbers 1 through 10 in column A of a worksheet.
- Type the formula in cell B2. When you get to the “n”, click on cell A1.
- Press Enter, then grab the little square at the right hand corner of B2. Drag this square to the bottom of column B2.
- The limit inferior is the smallest limit of a subsequence.
- The limit superior is the largest limit of a subsequence.
Step 2: Identify the pattern. We have two subsequences here: odd numbers where the limit is 2 and even numbers where the limit is 0. Therefore, the subsequential limits are 0 and 2.
Example question #2: Find the subsequential limits of the sequence an = 1 – (-1)n.
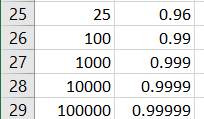
Step 1: Generate some terms of the sequence. For this example, I didn’t see a pattern for the first ten terms, so I went much larger:
Step 2: Identify the pattern.The sequence (and all of its subsequences) converge to 1. This is an example where it may be easier to demonstrate the limit with algebra. We know that |an| = 1/n → -, so an → 1.
The limits of subsequences can more formally be defined by the limit inferior and limit superior.
Limit Inferior & Limit Superior
The limit inferior and limit superior of a sequence give bounds on the sequence’s subsequential limits (i.e. the limit of a subsequence) [1]:
For bounded sequences, these limits always exist [2].
In notation, the limit inferior may be written as:
The limit superior may be written as:
Visual Example of Limit Inferior and Limit Superior
The bounded sequence ai = (-1)i(i + 1)/i is not convergent.
However, two subsequences (odd terms and even terms) are convergent, as shown on the following graph:
From the graph, we can see that the subsequence of even terms converges to 1, which means that the limit superior = 1. The limit inferior converges from below to -1. These limits give a qualitative measure of a sequence’s asymptotic behavior [3].
Another example is the (relatively) famous divergent sequence (1, -1, 1, -1, 1,…). While the sequence as a whole does not converge, the even terms converge to -1 (i.e. lim inf = 1) and the odd terms converge to 1 (lim sup = 1).

Graph of divergent sequence 1, -1, 1, -1,… with limit inferior (red) and limit superior (black).
Formal Definition
The limit inferior for a sequence xncan more formally be defined as follows:
The limit superior can be defined in a similar way:
The limit inferior is always smaller than the limit superior, unless the sequence is convergent. If that happens, then the two limits are equal. In notation, we can say:
lim inf ≤ lim sup.
References
Sequence Images: Desmos.
[1] Basic properties of limit inferior and limit superior. Retrieved May 3, 2021 from: https://www.uio.no/studier/emner/matnat/math/MAT1100/h20/grublelimsup.pdf
[2] Lebl, J. Basic Analysis I & II: Introduction to Real Analysis, Volumes I & II. 2.3 Limit superior, limit inferior, and Bolzano–Weierstrass. Retrieved May 3, 2021 from: https://www.jirka.org/ra/html/sec_bw.html
[3] Chidume Chapter 5. Retrieved May 3, 2021 from: http://www.math.utoledo.edu/~dwhite1/d_makerere/Chidume2.pdf
[4] Upper and Lower Limits of Sequences of Real Numbers. https://faculty.math.illinois.edu/~r-ash/RV/RV3.pdf
Stephanie Glen. "Limit Inferior, Limit Superior and Subsequential Limits" From CalculusHowTo.com: Calculus for the rest of us! /limit-inferior-and-limit-superior/
Need help with a homework or test question? With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is free!